Τέχνη & Μαθηματικά

Συνδυάζοντας το προοίμιο της Ιλιάδας με το απόφθεγμα του Πυθαγόρα «Σχάμα και βάμα» που σε ελεύθερη μετάφραση σημαίνει «κάθε νέο σχήμα είναι ένα βήμα προς τη γνώση» η στήλη φιλοδοξεί να ασχοληθεί με τους τρόπους που οι τέχνες αναζητούν την έμπνευση στους δαιδάλους των μαθηματικών

Παρόλο που δεν έχω εκπαιδευτεί και δεν έχω καμία γνώση στις θετικές επιστήμες συχνά μου δημιουργείται η εντύπωση ότι έχω περισσότερα κοινά με τους μαθηματικούς παρά με τους συναδέλφους μου καλλιτέχνες.

Στο δικτυακό τόπο του πανεπιστημίου Saint Andrews, την εγκυρότερη σήμερα πηγή μαθηματικών βιογραφιών, θα βρει κανείς ανάμεσα στα ονόματα του Αρχιμήδη, του Φερμά, του Όιλερ, του Γκάους και αυτό του Έσερ. Υπερβολική αβρότητα προς ένα καλλιτέχνη που χωρίς να είναι μαθηματικός τίμησε με το έργο του όσο κανένας άλλος τη μαθηματική επιστήμη; Ίσως. Σίγουρα ο Έσερ δεν ήταν μαθηματικός με τη συμβατική έννοια του όρου, δεν σπούδασε μαθηματικά, δεν τα δίδαξε, δεν δημοσίευσε κανένα ερευνητικό ή διδακτικό πόνημα πάνω σ’ αυτά. Ωστόσο πάμπολλα εγχειρίδια μαθηματικών περιλαμβάνουν έργα του, όχι ως απλά διακοσμητικά στοιχεία, αλλά ως εποπτικά μέσα για τη διδασκαλία του αντικειμένου. Και αρκετοί είναι εκείνοι που υποστηρίζουν ότι με το έργο του έχει συμβάλει, με αντισυμβατικό ίσως τρόπο αλλά πάντως ενεργά, στην πρόοδο των μαθηματικών.

Όταν πήγαινα σχολείο στο Άρνεμ ήμουν πολύ αδύνατος στην αριθμητική και την άλγεβρα γιατί είχα, και εξακολουθώ να έχω, μεγάλη δυσκολία με τις αφηρημένες έννοιες των αριθμών και των γραμμάτων. Αργότερα με τη στερεομετρία, που έβρισκε αντίκρισμα στη φαντασία μου, τα πήγα κάπως καλύτερα αλλά ποτέ στο σχολείο δεν διακρίθηκα σε αυτό τον τομέα. Ωστόσο η ζωή ακολουθεί συχνά παράξενες διαδρομές…

Αναμφίβολα ο Έσερ, στα δυο του ταξίδια το 1922 και το 1936 στην Ισπανία, όταν αφιέρωνε ολόκληρα εικοσιτετράωρα στη μελέτη των αραβικών διακοσμητικών μοτίβων του ανακτόρου της Αλάμπρα, δεν υποπτευόταν ότι αυτό που διεξήγαγε ήταν πρωτογενής μαθηματική έρευνα. Οι κανονικές πλακοστρώσεις του επιπέδου, οι διαφορετικοί δηλαδή τρόποι να καλυφθεί το επίπεδο με την περιοδική επανάληψη του ίδιου σχήματος, χωρίς κενά και επικαλύψεις, ήταν μια από τις διεξόδους που αναζήτησαν οι Μαυριτανοί καλλιτέχνες που η δημιουργικότητά τους ασφυκτιούσε κάτω από την απαγόρευση οποιασδήποτε αναπαράστασης ανθρώπων ή ζώων που επέβαλλε το Κοράνι.

Ως την «πλουσιότερη πηγή έμπνευσης» που είχε ποτέ, περιέγραψε ο Έσερ την τεχνική της πλακόστρωσης, την «κανονική διαίρεση του επιπέδου» όπως την αποκαλούμε σήμερα. Μάλιστα ο ίδιος, μην έχοντας θρησκευτικούς περιορισμούς δε δυσκολεύτηκε καθόλου να εφαρμόσει τους βασικούς επίπεδους μετασχηματισμούς (παράλληλη μετατόπιση, στροφή, ανάκλαση, ολισθαίνουσα ανάκλαση) σε εικόνες ανθρώπων, αλόγων, ψαριών και πουλιών. Αυτός δηλαδή που ισχυριζόταν ότι αδυνατεί να κατανοήσει τη μαθηματική αφαίρεση κατόρθωσε να ξεχωρίσει τη δομή από το περιεχόμενο και να αναπαραγάγει την πρώτη αλλάζοντας το δεύτερο.

Έτσι όταν το 1937 ο αδελφός του Μπέρεντ του έδωσε να διαβάσει το άρθρο του Γκέοργκ Πόλυα για τις ομάδες συμμετριών του επιπέδου, ο Έσερ, παρόλο που δεν αντιλαμβανόταν την αφηρημένη έννοια της ομάδας, δε δυσκολεύτηκε να κατανοήσει τη βασική ταξινόμηση των κανονικών διαιρέσεων του επιπέδου σε 17 κατηγορίες, ούτε και να συλλάβει πρακτικά, χωρίς τους αντίστοιχους μαθηματικούς φορμαλισμούς, τη δομή των 17 ομάδων συμμετρίας. Ήταν η πρώτη μαθηματική συνάντηση του Έσερ, που είχε ως συνέπεια μια ιδιαίτερα παραγωγική περίοδο, από το 1937 ως το 1941, κατά την οποία δημιούργησε 43 έγχρωμα σκίτσα προσεγγίζοντας με έναν εξαιρετικά συστηματικό τρόπο τις διάφορες ομάδες συμμετρίας και υιοθετώντας ένα δικό του «μαθηματικό» συμβολισμό. Στα επόμενα χρόνια δημιούργησε ξυλοτυπίες πειραματιζόμενος και με τις 17 ομάδες συμμετρίας του επιπέδου ανακαλύπτοντας στην πράξη όσα η μαθηματική ανάλυση είχε ήδη προβλέψει. Σ’ αυτό ακριβώς το σημείο εντοπίζει ο ίδιος τη διαφορά του έργου του από αυτό των μαθηματικών:

Στους κύκλους των μαθηματικών η κανονική διαίρεση του επιπέδου έχει αναλυθεί θεωρητικά […]. Οι μαθηματικοί έχουν ανοίξει μια πύλη που οδηγεί σε μια απέραντη επικράτεια, χωρίς ωστόσο να εισέλθουν οι ίδιοι στην επικράτεια αυτή. Από τη φύση τους, ενδιαφέρονται περισσότερο για τον τρόπο με τον οποίο μπορεί να ανοίξει αυτή η πύλη παρά για τον κήπο που κρύβεται πίσω της.

Παρά τους διαφορετικούς τους στόχους, μαθηματικοί και καλλιτέχνες φαίνεται πως μοιράζονται ένα κοινό χαρακτηριστικό: την τάση γενίκευσης. Δυο δρόμους μπορούσε να ακολουθήσει κανείς για να γενικεύσει. Πρώτον να ασχοληθεί με την κανονική διαίρεση του τρισδιάστατου χώρου και δεύτερον να στραφεί στη μη κανονική διαίρεση του επιπέδου, σε πλακοστρώσεις δηλαδή κατά τις οποίες τα «πλακάκια» εκτός από τις συμμετρίες υφίστανται και μετασχηματισμούς που δεν τα αφήνουν αμετάβλητα, όπως είναι η μεγέθυνση και σμίκρυνση.
Σημαντικό ρόλο στη στροφή του προς αυτή τη νέα κατεύθυνση έπαιξε η δεύτερη σημαντική μαθηματική του συνάντηση, με τον Αγγλοκαναδό γεωμέτρη Ντόναλντ Κόξετερ. Γνωρίστηκαν το 1954, στο Διεθνές Συνέδριο Μαθηματικών του Άμστερνταμ και δέθηκαν με μια στενή φιλία που κράτησε μέχρι το θάνατο του καλλιτέχνη το 1972. Από τις συζητήσεις του με τον Κόξετερ, ο Έσερ γνώρισε την υπερβολική γεωμετρία και τον τρόπο με τον οποίο μπορεί κανείς να την χρησιμοποιήσει για να απεικονίσει το άπειρο.
Πιθανότατα ο Κόξετερ να ήταν αυτός που έπαιξε το ρόλο του «διαμεσολαβητή» για μια εντυπωσιακή συνάντηση –στο χώρο των ιδεών– του Έσερ με τον κορυφαίο Γάλλο μαθηματικό Ανρί Πουανκαρέ.

Ο Πουανκαρέ και ο Έσερ δε συναντήθηκαν ποτέ ως φυσικά πρόσωπα, μια και ο πρώτος πέθανε το 1912, την εποχή που ο δεύτερος ήταν μόλις 14 ετών. Μάλιστα δεν έχουμε καμιά ένδειξη ότι ο Έσερ διάβασε ποτέ κάποιο κείμενό του. Ωστόσο φαίνεται ότι κάποια στιγμή της ζωής τους, για διαφορετικούς λόγους, με διαφορετικά κίνητρα και ξεκινώντας από διαφορετική αφετηρία, είχαν την ίδια έμπνευση που την εξέφρασαν ο καθένας με τον δικό του τρόπο, με το δικό του προσωπικό εκφραστικό μέσο. Ο Πουανκαρέ μ’ ένα ονομαστό σήμερα πείραμα σκέψης και ο Έσερ με μια σειρά ξυλοτυπιών, τα «Όρια Κύκλου», Ι, ΙΙ, ΙΙΙ και ΙV. Δεν έχουμε παρά να διαβάσουμε το κείμενο του Πουανκαρέ από το βιβλίο του Επιστήμη και Υπόθεση και στη συνέχεια να το παραβάλουμε με τις αντίστοιχες ξυλοτυπίες:

Ας φανταστούμε ένα κόσμο που περικλείεται από μια σφαίρα και που υπόκειται στους πιο κάτω φυσικούς νόμους: Η θερμοκρασία είναι μέγιστη στο κέντρο και μειώνεται ομοιόμορφα καθώς απομακρυνόμαστε από αυτό για να φτάσει στο απόλυτο μηδέν στην επιφάνεια της σφαίρας που περικλείει τον κόσμο μας. […] Όλα τα σώματα σε αυτόν τον κόσμο έχουν τον ίδιο συντελεστή διαστολής, έτσι που το μήκος μιας ράβδου να είναι ανάλογο προς τη θερμοκρασία της. Τέλος, υποθέτουμε πως ένα αντικείμενο που μετακινείται από ένα σημείο αυτού του κόσμου σ’ ένα άλλο με διαφορετική θερμοκρασία, προσαρμόζεται αυτόματα στα θερμικά δεδομένα της νέας του θέσης. […] Έτσι, ένα αντικείμενο που μετακινείται, καθώς πλησιάζει την εξωτερική σφαίρα θα γίνεται όλο και μικρότερο.
Αν αυτός ο κόσμος είναι πεπερασμένος από τη σκοπιά της δικής μας γεωμετρίας, στους κατοίκους του θα φαίνεται άπειρος. Πράγματι, όταν αυτοί πλησιάζουν την εξωτερική σφαίρα ψύχονται και γίνονται όλο και πιο μικροί. Τα βήματά τους γίνονται και αυτά όλο και πιο μικρά κι έτσι δε μπορούν ποτέ να φτάσουν την εξωτερική σφαίρα.

Δεν αποκλείεται βέβαια ο Έσερ να ενημερώθηκε για τις ιδέες του Πουανκαρέ από τους άλλους μαθηματικούς φίλους του, ωστόσο η εικαστική απεικόνιση του μοντέλου της υπερβολικής γεωμετρίας είναι καθαρά δικό του έργο, έργο μάλιστα που όπως αποδείχθηκε το 1995 από τον ίδιο τον Κόξετερ είναι από μαθηματική άποψη «…απόλυτα σωστό μέχρι χιλιοστού… Κρίμα που ο ίδιος δεν έζησε αρκετά για να δει τη μαθηματική του δικαίωση».
Ωστόσο η συνάντηση του Έσερ με τον Κόξετερ είχε πολλά ακόμα να δώσει. Όταν ο κορυφαίος γεωμέτρης του δεύτερου μισού του εικοστού αιώνα, με ιδιαίτερο ενδιαφέρον στα πολύεδρα, συναντά τον κορυφαίο γραφίστα που ξέρει –έστω κι αν δεν το υποψιάζεται– να φιλτράρει τα μαθηματικά μέσα απ’ το δικό του φανταστικό κόσμο και να τα εμπλουτίζει με τρόπους οικείους μόνο σε αυτόν, τα αποτελέσματα δεν είναι μόνο άρτια από αισθητική άποψη, αλλά έχουν και πολλές επιστημονικο - φιλοσοφικές προεκτάσεις. Μελετώντας κανείς το άπειρο, τη σχετικότητα, τους συνεχείς μετασχηματισμούς μέσα από τα έργα του Έσερ δεν αρκείται στο θαυμασμό ή την εικαστική ικανοποίηση· μετασχηματίζει, αναβαθμίζει και εμπλουτίζει τις γνώσεις του γι’ αυτά.

 Μια ακόμα σημαντική μαθηματική συνάντηση του Έσερ ήταν αυτή με τον Άγγλο μαθηματικό Ρότζερ Πένροουζ. Μαζί συνέλαβαν την ιδέα του στρεβλού τριγώνου –του tribar– που αποτέλεσε τη βάση για τα ανέφικτα κτήρια του Έσερ. Τρία σημεία στο χώρο ορίζουν πάντα ένα επίπεδο και συνεπώς σε αντίθεση με το στρεβλό τετράπλευρο (το τετράπλευρο που οι τέσσερις κορυφές του δεν ανήκουν στο ίδιο επίπεδο) το στρεβλό τρίγωνο είναι ανέφικτο. Όταν όμως αναπαριστούμε τον τρισδιάστατο χώρο στο επίπεδο η παραβίαση των κανόνων της προοπτικής μπορεί να δημιουργήσει την ψευδαίσθηση ενός στρεβλού τριγώνου και μέσω αυτού την εικόνα ενός αυτοτροφοδοτούμενου καταρράκτη, μιας κυκλικής διαδρομής παντού ανηφορικής και παντού κατηφορικής, ενός πύργου που ενώ ανεβαίνεις «από μέσα», όταν φτάνεις επάνω είσαι «απ’ έξω».

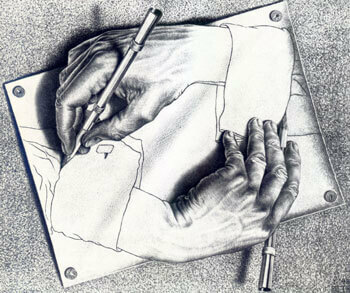
Η τελευταία μαθηματική συνάντηση του Έσερ είναι κι αυτή περιορισμένη στον κόσμο του νοητού. Δεν ξέρουμε αν ο Έσερ συναντήθηκε ποτέ με τον Ράσελ ή τον Γκέντελ. Ξέρουμε ωστόσο ότι και οι τρεις τους ασχολήθηκαν με την αυτοαναφορικότητα. Ο Ράσελ για να καταδείξει την αντίφαση που ενυπάρχει στην έννοια του «συνόλου όλων των συνόλων που δεν περιέχουν τον εαυτό τους», ο Γκέντελ για να αποδείξει ότι μια θεωρία δε μπορεί από μόνη της να εξασφαλίσει τη μη αντιφατικότητά της και ο Έσερ για να δημιουργήσει δυο πανέμορφα χέρια που ζωγραφίζουν το ένα το άλλο. Κι αν η αυτοαναφορικότητα είναι βραχνάς για τους μαθηματικούς, αφού κλονίζει τα θεμέλια της επιστήμης τους, ο Έσερ με τα χαρακτικά του τους στέλνει ένα αισιόδοξο μήνυμα: «Αν δεις τα πράγματα από τη σωστή τους διάσταση, όλα τα παράδοξα είναι απλώς ψευδαισθήσεις».

Πληροφορίες

[1] Η επίσημη ιστοσελίδα του Ιδρύματος M. C. Escher : https://www.mcescher.com/
[2] Μαγνητοσκοπημένη διάλεξη του καθηγητή Γ. Μπαλόγλου όπου αναλύεται εκτενώς το μαθηματικό περιεχόμενο του έργου του Escher, εδώ: https://www.youtube.com/watch?v=NrLVWEQ6uv0
[3] M. C. Escher : The Graphic Work. Κυκλοφορεί μεταφρασμένο σε πολλές γλώσσες. Περιλαμβάνει τα κυριότερα έργα του χαράκτη με σχόλια από τον ίδιο.
[4] Τεύκρος Μιχαηλίδης: Ο μέτοικος και η συμμετρία. Μυθιστόρημα στο οποίο ο Έσερ είναι ένας από τους βασικούς χαρκτήρες.